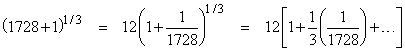The Dullness of 1729

One of the best-known anecdotes in the history of mathematics is about a visit that Hardy paid to Ramanujan in the hospital in 1917. The latter had been an obscure young clerk in his native India until just a few years earlier, when he had written to Hardy - then the world's most famous mathematician - asking Hardy to look at some of his work.  Hardy immediately recognized that the young man had an extraordinary gift, and arranged for Ramanujan to go to Cambridge in 1913.  The work that Ramanujan did there between 1913 and 1918 is legendary.  Unfortunately, he fell ill in 1917, and thereafter spent much of his time in the hospital.  He seems to have believed that his health problems were due to an inability to get suitable food in England, (he was a strict vegetarian, and cooked all his food himself), so in 1919 he returned to India.  Alas, his health did not improve, and he died in 1920.

The famous anecdote is that during one visit to Ramanujan in the hospital at Putney, Hardy mentioned that the number of the taxi cab that had brought him was 1729, which, as numbers go, Hardy thought was "rather a dull one".  At this, Ramanujan perked up, and said "No, it is a very interesting number; it is the smallest number expressible as a sum of two cubes in two different ways."  This was the sort of thing that prompted Littlewood to say "every positive integer was one of [Ramanujan’s] personal friends".

I was reminded of this story after noticing that, beginning at the 1729th decimal digit of the transcendental number e, the next ten successive digits of e are 0719425863.  This is the first appearance of all ten digits in a row without repetitions.  So if anyone ever tells me that 1729 is a dull number, I intend to affect a moment of contemplation and then say "Not at all, it is the first occurrence of all ten digits consecutively in the decimal representation of e". Now that’s impressive.

But seriously, it's always seemed implausible to me that Hardy thought 1729 was a dull number.  In addition to being the smallest number that is a sum of two cubes in two distinct ways, it's also a Carmichael Number, i.e., a pseudoprime relative to every base. The first three Carmichael Numbers are 561, 1105, and 1729.  (It's interesting that 1105 is expressible as a sum of two squares in more ways than any smaller number, and of course 561 is expressible as a sum of two first-powers in more ways than any smaller number.)

Incidentally, Hardy told the story about 1729 as part of his answer to the question of "whether [Ramanujan's] methods differed in kind from those of other mathematicians; whether there was anything really abnormal in his mode of thought." Hardy's answer was that, although Ramanujan's memory and powers of calculation were very unusual, they could not reasonably be called "abnormal". He (Hardy) believed that "all mathematicians think, at bottom, in the same kind of way, and that Ramanujan was no exception". To illustrate this point, he then told the story about 1729, but significantly he says that after hearing Ramanujan's observation on 1729 he (naturally) asked if he knew of any number expressible as a sum of two fourth powers in more than one way. "[Ramanujan] replied, after a moment's thought, that he could see no obvious example, and thought that the first such number must be very large." Hardy didn't mention, but quite possibly knew by the time he wrote about this incident, that Euler had found (more than a century before) an infinite family of such numbers, the first of which is

So, although the story of 1729 is usually presented as an example of Ramanujan's unusual prowess, it seems that Hardy intended the overall anecdote to show not only Ramanujan's capabilities, but also his limitations. Had Ramanujan pondered for a moment and announced the number 635318657, presumably Hardy would have been ready to describe his mode of thought as being "abnormal".

The number 1729 also appears in Richard Feynman's collection of anecdotes (Surely You're Joking, Mr. Feynman!). In a chapter entitled "Lucky Numbers" he tells of going into a small restaurant in Brazil to eat lunch. He's the only customer, so he has four waiters standing around him. Then a Japanese man enters the restaurant, and he is selling abacuses. The man challenges the waiters to an adding contest, but they don't want to lose face, so they tell him to go challenge the customer sitting there (Feynman). They first have an addition contest, and the abacus wins easily. Then they try multiplication, and the abacus wins again, but it's a bit closer. Then they try long division, and this time it's a tie. As Feynman says, the more difficult the problem, the better he can do with pencil and paper compared with the abacus. Finally the Japanese man calls out "Raios cubicos!"... he wants to challenge Feynman to cube roots.

Feynman says the man wrote a number, "any old number", down on a piece of paper, and he still remembers the number... 1729.03. The salesman begins working furiously on his abacus, but Feynman just sits there smiling, and says "12.002...". The abacus salesman was beaten, and left the restaurant in disgust. The waiters are amazed at Feynman's calculating prowess. He explains that he happened to remember that there are 1728 cubic inches in a cubic foot, so the cube root of 1729 must be just slightly greater than 12. Then he just needed to account for the extra 1.03. To do this he neglected the 0.03 and used the binomial expansion

so the amount by which the cube root of 1729 exceeds 12 is about 4/1728 = 1/432. You can only get two 432's out of 1000, so the first non-zero digit is 2, leaving a remainder of 136, and bringing down another zero we know there are three 432's in 1360, so the next digit is 3, and so on. This gives 12.0023... 

Feynman's book contains many stories similar to this, in which he is able to perform a seemingly difficult mental feat, and he then explains that it was only by luck that he happened to recognize something about the problem that made it simple. He says Hans Bethe was an even better mental calculator, and by similar means. Feynman says "It was easy for him - every number was near something he knew".

Return to MathPages Main Menu