|
Thinking Outside the Triangle |
|
|
|
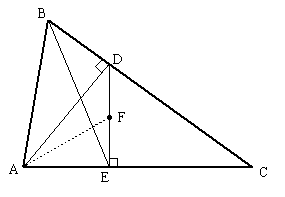
Given an arbitrary triangle ABC, let D be the foot of the perpendicular from A to BC, let E be the foot of the perpendicular from D to AC, and let F be a point on the line DE, as illustrated below |
|
|
|
|
|
|
|
Florin Pirvanescu challenged the readers of Mathematics Magazine in June 1991 to prove that AF is perpendicular to BE if and only if FE/FD = BD/DC. Several proofs have appeared, based on synthetic, projective, and vector methods. These proofs are all fairly elaborate, but there is actually a very simple elementary proof, which is a nice example of "thinking outside the box". |
|
|
|
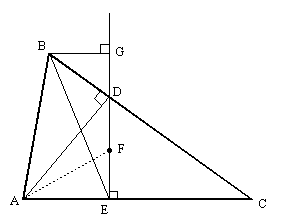
Let G be the foot of the perpendicular from B to DE, as shown below. |
|
|
|
|
|
|
|
Clearly BDG ~ DAE and DGE ~ DBC, so we have BG/DG = DE/AE and EG/DG = CB/DB. Also, AEF ~ EGB, giving EG/BG = AE/FE, if and only if AF is perpendicular to BE. Thus we have |
|
|
|
|
|
|
|
which implies DE/FE = EG/DG = CB/DB and so FED ~ DBC if and only if AF is perpendicular to BE. |
|
|