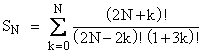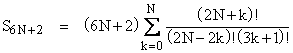Summations and Recurrences

Consider the sum

 For example, we have

and so on. Is S_n ever an integer for any positive integer n? The answer is yes, but the first occurrence of an integer in this sequence is S_2755452, which is an integer having just over 2 million digits. This is related to the fact that n = 6(2755452) + 2 is the smallest pseudoprime of the form 6N + 2 relative to the cubic polynomial x³ - x - 1.

For any integers m,n with m greater than or equal to n, define

where C(m,n) = m!/[n!(m-n)!] is the binomial coefficient. We also define F(m,n) = 0 if m < n or n < 0. Since the F coefficients are just a linear function of the binomial coefficients they clearly satisfy the same recurrence, i.e.,

Now, for any non-negative integer N, define

It follows that for any integer q > 2 we have the recurrence

To prove this, first consider the case where q is odd. In that case we can put q = 2N + 1 and the recurrence can be written as

By the definitions of S_2N and S_2N+1 this relation is

which follows immediately from (1) for each k. On the other hand, if q is even, we can put q = 2N and the recurrence can be written as

which by definition is

By a shift of index the second sum on the right side can be written as

and since F(N-1,-1) = 0 the summation can be carried over k ≥ 0, so again we can apply relation (1) for each k to give the result.

We now consider the values of S(6N+2) for any positive integer N. By definition we have

Also, from the definition of F(m,n) we have

Therefore we have

If we evaluate the terms in the summation in reverse order by substituting N - k for each k, we have the equivalent expression

Consequently, the summation in question is an integer if and only if S_6N+2 is divisible by 6N+2. Now, recall that

for all n > 2, and we have the initial values S₃ = 3, S₄ = 2, and S₅ = 5. These happen to be the values that would result from the initial values S₀ = 3, S₁ = 0, and S₂ = 2, so the entire sequence consists of Newton’s sums for the roots of the cubic

and by Fermat's theorem we immediately know S_p = S₁ = 0 (mod p) and so S_p is divisible by p for every prime p. However, composite integers n such that S_n is divisible by n are quite rare. These are called pseudoprimes relative to the cubic (2). We are seeking a pseudoprime of the form n = 6N + 2. To prove that N = 2755452 gives such a number, we need only show that S_n = 0 (mod n) for n = 6(2755452) + 2 = 16532714. The nth term of any linear recurring sequence (mod n) can be evaluated in log(n) steps (using binary exponentiation), so it's not hard to verify that S_16532714 = 0 (mod 16532714). This is in fact the smallest even pseudoprime relative to (2).

Return to MathPages Main Menu