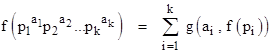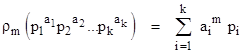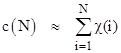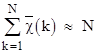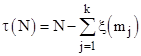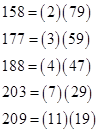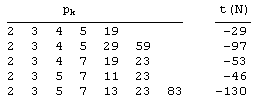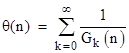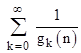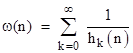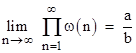Part 5:  Miscellaneous Related Results

Generalized Additive Functions:  In the definition of  ξ(n)  we imposed the requirement that for any integers x and y the additive property

was satisfied. If we relax this requirement so that the additive property only needs to apply to any two co-prime integers x and y, then a slightly larger family of functions is possible. These functions must satisfy f(1) = 0 and

where g and f are any integer-valued functions, not necessarily linear. If, as before, we set f(p_i) = p_i , and then we define g(a,p) = a^mp for some fixed integer m, then we have the family of additive functions

Thus, ρ₀(N) is the sum of distinct prime factors of N, and ρ₁(N) = ξ(N) is the sum of all the prime factors. To illustrate, for N = (2)²(3) = 12 we have

ρ₀(12) = 2⁰(2) + 1⁰(3) = 5

ρ₁(12) = 2¹(2) + 1¹(3) = 7

ρ₂(12) = 2²(2) + 1²(3) = 11

The only completely additive member of this family is ρ₁. If N is square-free, meaning all the exponents in the prime factorization are 1, we have ρ_k(N) = ρ₀(N) for all k. Therefore, any solution set for ρ₁ consisting of square-free integers is also a solution set for every ρ_k function.

The Density of G Forms:  It's interesting that the total number of representations in the form n + ξ(n) for all the integers n less than or equal to N follows very closely the number of composite integers less than or equal to N. Letting c(N) denote the number of composites less than or equal to N, we have

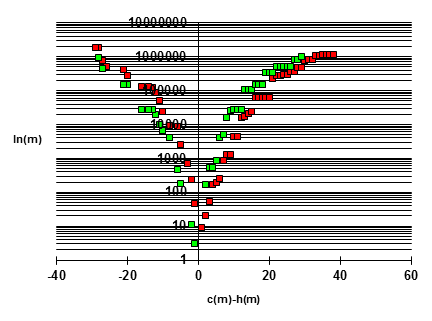
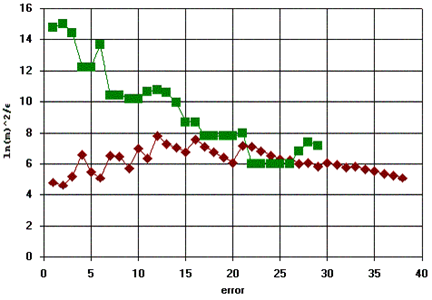
Notice that for each prime p we have p + ξ(p) = 2p, which implies that none of the primes greater than N/2 contribute to the summation. On the other hand, all the integers less than N/2, prime and composite, contribute to the summation. Therefore, to make the preceding approximation true,  the number of primes less then N/2 must approximately equal the number of "excluded composites" greater than N/2. In other words, if w(x) signifies the number of integers k less than x and such that k + ξ(k) > x, then π(x) ~ w(2x). Table 7 gives the "new greatest errors", positive and negative, for all m up to 2000000. This is plotted in the figure below.

The figure below presents a plot of ln(x)²/w(x)  vs  the "error"  |w(x) − π(x/2)|.

This figure suggests that

A related observation has to do with the "conjugate" function

We will denote by  the valence of  on n. Clearly for every prime p we have

so it follows that

If we tabulate the valencies of  on k for all the integers k from 1 to N we find that

This implies that, since the primes are absent from these valencies, the number of composites k greater than x and such that k − ξ(k) < x must be approximately equal to the number of primes less than x.

In summary, we have found two approximations to π(x):

π(x) ~ number of composites k less than 2x such that k + ξ(k) > 2x

π(x) ~ number of composites k greater than x such that k ξ(k) < x

Both of these approximations for π(x) are in terms of the composites in the range from x to 2x. The first counts the number of composites in this range that, when the sum of their prime factors is added, fall outside the range. The second counts the number of composites in this range that, when the sum of their prime factors is subtracted, fall outside the range. Table 9 gives the valence statistics of   for all m up to 100.

Every integer of the form n = p − 2 has  -valence of at least 1, because of the integer 2p. This is analogous to the fact that every integer of the form m = 2p has G-valence of at least 1, because of the integer p.

Negative Values of τ(m):  Recall from Section 4 that, given the set of integers {m₁,m₂,..,m_k} for any given N such that  m_j + ξ(mj) = N, the function τ(N) was defined as

It was noted that τ(N) is positive for nearly all N, and the average value of τ(N) increases as N increases. In fact, for positive values of τ(N) it seems that for any x there is an integer k such that τ(N) > x  for all N > k. However, for a small number of integers N the value of τ(N) is negative. The first such value (and the only one less than 500) is 239, for which τ(239)= −21. Table 8 lists the only other occurrences of negative τ(m) for m less than two million.

Since the value of  τ(c) = c − Σξ(n_i) can be positive or negative, it's natural to wonder if it is ever zero, giving b = 1 with no common factors in the n_i, which would imply the existence of a set of primes of which the s_i constitute a natural partition and there would be no need to augment the set S with "inert" primes. Table 8 does not provide an example of this phenomenon. It is not known if τ(N) = 0 for any integer N, but we can make some general observations on the behavior of τ(N) that place severe constraints on any such N.

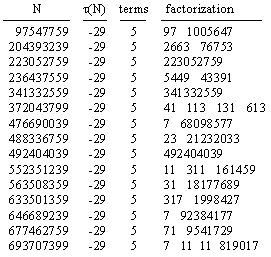
Jud Mccranie numerically checked integers up to 10⁹ and found no cases with τ = 0, but he did continue to find occasional integers with relatively small negative values of τ. (He found about 2000 in all.)  Interestingly, only a certain set of negative values occur, and these occur repeatedly. For example, we have the following 15 integers in this range with the τ(N) = −29:

It isn't difficult to see that this is a consequence of the existence of certain partitions of 1 into Egyptian unit fractions. Suppose we can find an integer N such that each of the following five numbers is a prime:

It follows that m + ξ(m) = N  where m is any of the five numbers 2a, 3b, 4c, 5d, 19e. If no other "m value" exists for this N, then τ(N) = −29.

What's so special about the set of numbers {2,3,4,5,19}?  Remember that according to the definition of τ(N) we have

Substituting the above expressions for a,b,c,d,e and separating terms we have

The sum of the unit fractions in the first parentheses is 1, and the sum of the complement fractions in the second parentheses is 4, giving the result τ(N) = −29  independent of N. So it turns out the ancient Egyptian fractions play an important part in this phenomenon. To make this work for some number besides −29 we would need to find another sum of distinct unit fractions that sum to 1, and whose denominators are all 1 greater than a prime (counting 4 as a prime because ξ(4) = 4). Let's say we have a set of k distinct primes {p₁,p₂,...p_k} (again allowing 4 to be considered as a prime) such that

and

It follows that if N is any integer such that each of the numbers

for j = 1,2,..,k is a prime integer then τ(N) = k − 1 − M. This effectively rules out finding an integer N of this form with τ(N)=0, because the sum of the k primes will clearly always be greater than k−1. Still, this is an interesting result in its own right.

This raises some interesting questions:  For any fixed set of primes {p1,p2,..,pk}, are there infinitely many N that give all prime values of (N − p_j)/(p_j + 1) for j = 1,2,..,k?  Also, are all negative values of τ members of families of this type?   The answer to this second question is no, because most of the integers with negative τ are demonstrateably not of this form. For example, the very first occurrence of a negative τ is τ(239) = -21, which has the set of "m values"

Thus 239 is an example of an integer N such that (N−2)/3, (N−3)/4, ..., (N−11)/12 are all primes (and no other m-values exist). For any such integer, we have

which reduces to

Notice that if N=2759 were such that (N−2)/3, ..., (N−11)/12 were primes, then it would give τ = 0. It actually happens that (2759−2)/3 and (2759−11)/12 are both primes, but the rest of the conditions are not satisfied, so τ(2759) does not equal zero. However, there doesn't seem to be any a priori reason why something like this couldn't eventually happen for some N, giving a τ of zero.

Returning to the families of equal τ values, I've identified the family for most of the persistent small negative values of τ. These correspond to the following sets of primes (again treating 4 as a prime):

Series Defined In Terms of G and H:  In a previous section the iterated functions G_k(n) and H_k(n) were defined, and we also discussed the analogous functions based on continuous logarithms h_k(x) and g_k(x). In each case we can consider the sums of the inverses of these monotonic functions. For example, we define

The corresponding function for g_k(x) gives a sum of inverses of quantities that grow at approximately the same rate as the prime numbers, i.e., the gap between two consecutive values y and y + Δy in the sequence is ln(y). On this basis we surmise that the sum

diverges (albeit very slowly). However, the rate of growth of G_k is fast enough to give a convergent sum. It's interesting that for any given integer n the sequence G_k(n) traces a monotonically increasing set of integers, and this "path" is joined at various points by other "paths". The points where two paths join are precisely the occurrences of two integers m,n such that G(m) = G(n) (which, as we have seen, correspond to families of solutions of H(N) = H(M)). Similarly, the points where multiple paths join correspond to higher order solution sets.

It is clear that if two integers n and m are "connected" in the sense that they lie on G-paths that ultimately join, then θ(n) − θ(m) is rational. Are all G-paths ultimately connected?  It appears that the number of separate strands increases very slowly (like log(x)).

The function

converges very rapidly, and it has the interesting property that

and the product

Symmetric Functions:  Although the ξ(n) function was introduced as an integer valued function possessing the Additive Property, it may also be regarded, along with n itself, as an elementary symmetric function of the constituent primes. This suggests consideration of the other elementary symmetric functions of those primes. We could denote by ξ_j(n) the sum of all products of j prime factors of n. These quantities are, of course, just the coefficients (up to sign) of the monic polynomial whose roots are the prime factors of n.

Return to Table of Contents