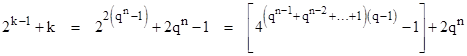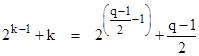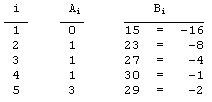Part 2:  Primes Related to Corollary 7.1

From Corollary 7.1 it follows that the only solution kernals n,m with n equal to a power of a prime are of the form

where k is any integer such that m is a prime. The only such values with k < 200 are:

The first two of these (with k = 1 or 3) do not give solution kernels because n ≤ 8 (see Proposition 7), but the pair m,n for k = 7 is a solution kernel.

When searching for primes of the form m = 2^k−1 + k we can immediately exclude all even values of k, because they give m divisible by 2. We can also exclude many other values of k, as described in the following propositions.

Proposition 8:  If k is odd and k−2 is divisible by exactly t powers of 3, then 2^k−1 + k  is also divisible by exactly t powers of 3.

Proof:  The premise implies that k = c3^t + 2, for some odd integer c co-prime to 3, so we have

Thus, we need only show that the quantity in parentheses is divisible by at least t + 1 powers of 3 for any non-negative integer t and odd integer c. Since c is odd, we can write c = 2d + 1 for some non-negative integer d. Then, with t = 0, the quantity in parentheses can be written

Noting that 4 = 1 (mod 3), it's clear that this quantity is divisible by 3 for any integer d. Therefore, the exponential term is congruent to −1 (mod 3), which allows us to write

where t = 0. Taking the cube of both sides gives

which shows that

is congruent to -1 modulo 3^t+2. Therefore, adding 1 to this quantity gives an integer divisible by 3^t+2. By induction, it follows that for every t, the quantity

is divisible by t+1 powers of t, which proves that the quantity

is divisible by exactly t powers of 3 (recalling that c is co-prime to 3). □

Proposition 9:  If qⁿ = (k+1)/2 is an odd prime power, then q divides 2^k-1 + k.

Proof:  The premise implies k = 2qⁿ – 1, so we have

The quantity in parentheses is congruent to 0 (mod q) by Fermat's Little Theorem, so the entire quantity is divisible by q. □

Proposition 10:  If  q = 2k + 1  is a prime, and 2 is a square modulo q, then q divides  2^k−1 + k.

Proof:  The premise implies  k = (q−1)/2, so we have

Multiplying by 2 gives

Thus, if 2 is a square modulo q, it follows that the quantity in brackets is congruent to 0 (mod q), so the entire quantity is divisibly by q. □

Proposition 11:  If k is of the form 20c + 9 or 20c + 11, then 2^k−1 + k is divisible by 5.

Proof:  If k = 20c + 9 then we have

Noting that 2⁴ = 1 (mod 5) and that 9 = −1 (mod 5), it follows immediately that this quantity is divisible by 5.

If k = 20c + 11, then we have

Noting that 2² = −1 (mod 5) and that 10c+5 is always odd, it's clear that the first term on the right side is always congruent to −1 (mod 5). Also, 11 is congruent to +1 (mod 5), so the entire quantity is divisible by 5. □

Discussion:  Proposition 11 can be generalized to give an infinite family of divisibility tests. Notice that the integers s_k = 2^k−1 + k satisfy the linear recurrence

with initial values s₁ = 2 and s₂ = 4. When the elements of this sequence are evaluated modulo the prime p, they are periodic with a period dividing τ_p = p(p−1). Thus, identifying the "zero terms" gives a set of arithmetic sequences such that if k is in one of these sequences, then s_k is divisible by p. This approach gives the following odd-valued arithmetic sequences:

With just these sequences we can exclude all k values less than 100 (other than 1, 3, and 7) except for k = 27, 43, and 67, all of which can be excluded by direct factorization. Indeed this approach allows us to determine that 2^k−1 + k is not prime for any other k (besides 1, 3, and 7) less than 200. The smallest integer k > 7 such that  m = 2^k−1 + k  is prime is 237, which gives the following 72-digit prime:

The next (probable) prime, found by H. Zeisel, corresponds to k = 1885, and for a long time this was the largest value of k known to yield a prime (or probable prime). Then, in November 1999, Nuutti Kuosa reported that he had tested up to 2^(51674−1) + 51674 and had found that 2^(k−1) + k is a probable prime with k = 51381. This prime has 15467 digits. Notice that suitable k values are more rare than suitable Mersenne exponents, because the simple divisibility conditions described above exclude large classes of k values. These criteria can be summarized as follows:

(i)         If k is even, then so is s_k.

(ii)        If k−2 is odd and divisible by n powers of 3, then s_k is also divisible by n powers of 3.

(iii) If qⁿ = (k+1)/2 is a power of a prime q, then q divides s_k.

(iv) If q = 2k+1 is a prime, and 2 is a square (mod q), then q divides s_k.

(v)        For any odd prime p with w = ord_p(2), there are w residues r modulo pw such that if k = r modulo pw then p divides s_k.

To elaborate on criterion (v), notice that for any prime p we can consider whether there exists a number q such that

for every integer j. In other words, 2^(k-1) + k  is divisible by p whenever k is congruent to q modulo p(p−1). The modulus p(p−1) was chosen so that it has the two properties of being zero mod p and being an exponent that gives unity mod p (by Fermat's Little Theorem). Obviously since 2^(p-1) = 1 (mod p), and since jp(p-1) = 0 mod p, we can reduce the above to simply

Hence if we can find an integer q that satisfies (2), then it also satisfies (1) for every j.

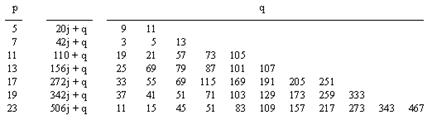
Now, for every odd prime p there are p−1 integers q in the range 1 to p(p−1)−1 that satisfy congruence (2). A table of these q values for the first few odd primes is given below:

Of course, in practice we can omit the even values of q (which comprise exactly half of the values), because they yield an even value of k. The values of q for any given prime p represent a closed set (mod p) of powers of 2 times one particular base. For example, with p = 11 the values of q reduced modulo p are {3, 8, 10, 9, 4, 1, 2, 5, 7, 6} respectively, which represents a complete set of non-zero residues mod 11. These can be arranged as a geometric series in powers of 2 (mod 11) as follows: {1, 2, 4, 8, 5, 10, 9, 7, 3, 6, 1, ...}, where each number is 2 times the previous number in the cycle. Since the order of 2 (mod 11) is 10, we get all 10 residues.

However, this isn't always the case. For example, with p = 7 the reduced q values modulo 7 are {3, 5, 6, 3, 5, 6}, which represents only half of the non-zero residues (mod 7), but as always this is a complete cycle under doubling, because 2(3) = 6, 2(6) = 5, and 2(5) = 3, all modulo 7. Hence, although there are p−1 distinct q values in the range 1 to p(p−1)−1, the number of distinct residue classes (mod p) represented among these q values is just equal to the order of 2 (mod p), i.e., the smallest exponent w such that 2^w = 1 (mod p).

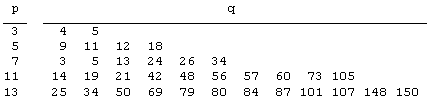
An extreme example of this is with p = 31, where we have 30 values of q that satisfy (2), but these fall into only 5 distinct residue classes modulo 31 because the order of 2 (mod 31) is just 5. Here's a summary of these q values.

These q values can be expressed in the form

where j ranges from 0 to 5, and w_p is the order of 2 (mod p), and the coefficients are

Notice that the values of B_i (which are just the reduced values q mod p) are precisely the negatives of the powers of 2 (mod p).

For another example, with p = 43, the order of 2 (mod 43) is w₄₃ = 14, so the 42 suitable values of q are given by equation (3) with j ranging from 0 to 2 (the upper index 2 being (p−1)/w_p − 1) and with the coefficients

In general, to satisfy the congruence 2^q−1 + q = 0 (mod p) we have q = −2^(q−1) (mod p), which means there exists an integer "a" such that

Also, the exponent q−1 on 2 will give a distinct result (mod p) only for distinct residues of q−1 modulo the order of 2 (mod p). Letting w denote this order, i.e., w = ord_p(2), we can set

for integers A, B, and m. Eliminating q from these two equations gives

(Notice that the right hand side of the above equation is of the form 2^j−1 + j.) So, for any prime p, we set w equal to the order of 2 (mod p), and then we solve the above linear equation with m = 0, 1,.., q−1. For each of these values of m, we take the smallest (p−1)/w solutions, and from those B values we compute q = 1 + m + Bw. This gives all p−1 values suitable values of q modulo p(p−1), but we can reduce this by just considering the suitable values modulo pw, of which there are exactly w.

For example, with p = 31 we have w = 5, and the minimal solutions of

with m = 0, 1, 2, 3, and 4 are (A,B) = (2,12), (4,24), (2,11), (2,10), and (1,2) respectively. From the relation q − 1 = m + Bw we then infer that the suitable values of q are any numbers congruent modulo 155 to 61, 122, 58, 54, and 15 respectively. In other words, we have found that 2^k−1 + k is divisible by 31 if k is any number of the form 155n+15, 155n+54, 155n+58, 155n+61, or 155n+122. For example, setting k=15 gives 2^k−1 + k = 16399 = (31)(529). Even for negative values of n, the numerator of the resulting reduced fraction is divisible by 31, as would be expected, because the denominator is a pure power of 2, which is coprime to 31, so the divisions are unique modulo p.

Return to Table of Contents