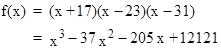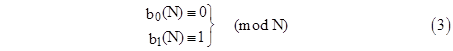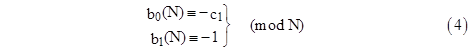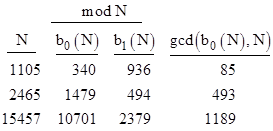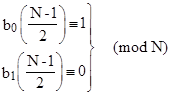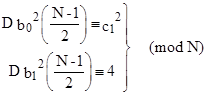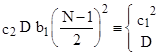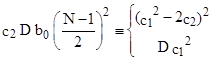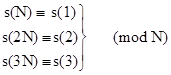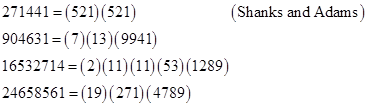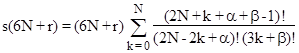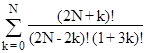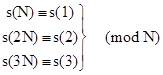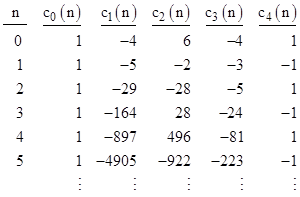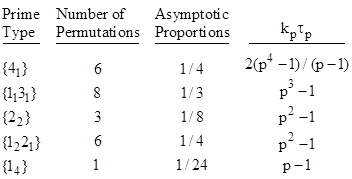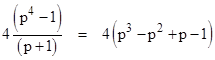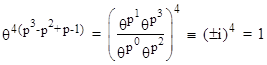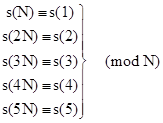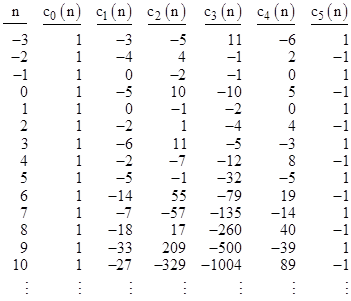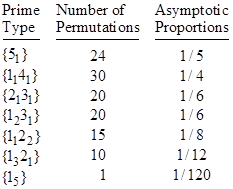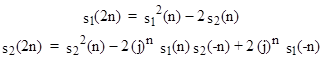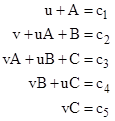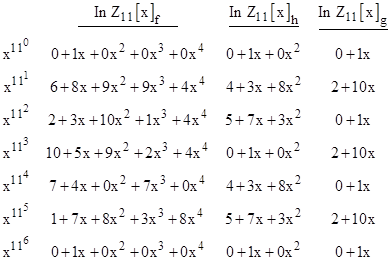2  Symmetric Pseudoprimes Relative to Selected Polynomials

This section presents examples of symmetric pseudoprimes relative to selected polynomials of degrees 1 through 5. For degrees 1, 2, and 3 the discussion focuses on familiar polynomials (such as the Fibonacci polynomial of degree 2 and Perrin's polynomial of degree 3) to show how these well known cases fit within the context of symmetric pseudoprimes. For higher degrees there do not appear to be such well established examples, so we have focused on irreducible polynomials with small integer coefficients and a variety of splitting field structures. In particular, we exhibit a symmetric pseudoprimes relative to a fully symmetric quintic.

2.1  Polynomials of Degree 1

By Proposition 6, the symmetric pseudoprimes relative to any given first degree polynomial f(x) = x – c (c in Z) are the integers N such that s(N) = s(1) (mod N), which is to say, c^N = c (mod N). Therefore, the symmetric pseudoprimes relative to f are identical to the ordinary pseudoprimes relative to f.

All the symmetric pseudoprimes less than 10⁴ relative to the first degree polynomials f(x) = x – 2, f(x) = x – 3, and f(x) = x – 5 are listed in Table 1. The entries listed in bold are Carmichael numbers, which are symmetric pseudoprimes relative to every first degree polynomial. The entries listed in parentheses are those divisible by c.

The importance of imposing congruence conditions on all the symmetric functions (not just the sum) of the roots can be shown by considering products of first degree polynomials. For example, the ordinary pseudoprimes relative to the polynomial

include not only the integers that are pseudoprimes relative to both x – 2 and x – 3, but also the integers n for which 2ⁿ + 3ⁿ = 2 + 3 even though 2ⁿ ≠ 2 and 3ⁿ ≠ 3 (mod n). All such n less than 10⁶ are listed in Table 2. (The values listed in parentheses are those divisible by 2 or 3). Also shown are the values of 2ⁿ3ⁿ (mod n), demonstrating that of all these ordinary pseudoprimes only 15 is a symmetric pseudoprime; the others each satisfy the congruence condition on the first symmetric function (the sum), but not on the second summetric function (the product).

Table 3 gives the ordinary pseudoprimes less than 10⁶ relative to f(x) = (x – 2)(x – 3)(x – 5), excluding those that are pseudoprimes relative to all three of the individual polynomials x–2, x–3, and x–5. Notice that 50721 and 811921 satisfy the required congruence conditions on the third as well as the first symmetric function. Similarly, the integer 49 (not shown) satisfies the second and third congruence but not the first.

To complete the demonstration that no two of the congruences, for a general cubic, is sufficient to ensure that all three are satisfied, we need to show a case that satisfies the first two but not the third. We have not found such a case relative to f(x) = (x – 2)(x – 3)(x – 5). However, relative to the polynomial

the composite integer N = 703 = (19)(37) satisfies the congruence s(kN) = s(k) (mod N) for k = 1 and 2, but not for k = 3. To prove this, we first form the Nth powers of the roots (mod N) as follows:

The elementary symmetric functions of these powers are

Since 498 = –205 (mod N), we see that s₁(N) = s₁(1) and s₂(N) = s₂(1) (mod N). However, 96 is not congruent to –12121 (mod N), so N is not a symmetric pseudoprime relative to f. This fact can also be shown in terms of the sequence of s₁(k) values (mod N) as follows

Thus, the three congrunces together are a stronger test than just the first two.

2.2  Polynomials of Degree 2

The odd symmetric pseudoprimes relative to any given second degree polynomial f(x) = x² + c₁x + c₂  (c_i in Z) are the composite integers N for which the congruences s(N) = s(1) and s(2N) = s(2) are both satisfied (mod N). Noting that s(0) = 2, s(1) = –c₁, and s(2) = c₁² – 2c₂, equation (23) from Section 1 allows us to express the conditions s(N) = s(1) and s(2N) = s(2) as follows

These and all other congruences in this section are understood to be (mod N) unless some other modulus is specified. Notice that if N is co-prime to 2c₁, then equation (1) implies

where gcd(u,v) signifies the greatest common divisor of u and v. Now, using the basis sequence relations described in Part 1 we can express b₀(2N) and b₁(2N) in terms of b₀(N) and b₁(N) as follows

Substituting these expressions into (2) gives

where the argument of each basis sequence symbol, when not explicitly specified, is understood to be N for the remainder of this section. Multiplying through by 2 and substituting the expression for 2b₀ from equation (1) gives

where D = c₁² – 4c₂, the discriminant of f. Clearly, the congruence is satisfied if b₁ = 1 (mod N), meaning that N divides b₁ – 1. On the other hand, if N and b₁ – 1 are relatively prime, then we can divide the preceding congruence by b₁ – 1 to give

In this case, assuming D is coprime to N, we have b₁ = –1 (mod N). Now, since (1) gives b₀ = (c₁/2)(b₁ – 1), it follows that for any prime or symmetric pseudoprime N co-prime to 2c₁D, and assuming that N either divides or is co-prime to b₀(N), we have

or

Of course, the divisibility assumptions on N used in this derivation are not implied by the definition of a symmetric pseudoprime, so the congruences (3) and (4) are a stronger primality criterion.

Definition 3:  A symmetric pseudoprime N relative to a second degree polynomial f is called determinate if gcd(2c₁D,N) = 1 and gcd(b₀(N), N) = 1 or N.

Clearly a determinate symmetric pseudoprime satisfies either (3) or (4). To further strenghten the criterion, we can specify which of these two conditions applies to any given N. If N is actually a prime, it follows from the discussion in Section 1.7 that equation (3) is satisfied if f splits into linear factors in the field Z_N (which implies that D is a square modulo N), and that equation (4) is satisfied if f is irreducible in Z_N (which implies that D is not a square modulo N).

To illustrate the preceeding topics, consider the familiar "Fibonacci polynomial"  f(x) = x² – x – 1. Since this is reversible, we know (by Proposition 8) that a composite integer N is a symmetric pseudoprime relative to f if and only if s(N) = s(1) (mod N). All 86 such composites N less than 10⁶ are listed in Table 4, along with the values of b₀(N) and b₁(N) (mod N), and gcd(N, b₀(N)). Nineteen of these symmetric pseudoprimes can immediately be distinguished from primes because they are not determinate (eleven being divisible by the discriminant D = 5, and eighteen having  1 < gcd(N, b₀(N)) < N ). Each of the remaining 67 symmetric pseudoprimes is determinate, but eleven of them (listed in parentheses) can be excluded because they exhibit the wrong congruences for their residue classes (mod 5). This leaves 56 composites which cannot be distinguished from primes based on any of the criteria discussed above.

There are second degree polynomials that exhibit a much lower density of symmetric pseudoprimes than the Fibonacci polynomial. For example, the polynomial

has only 4 symmetric pseudoprimes less than 10⁶, none of which is determinate. Notice that since this polynomial is not reversible, the single congruence s(N) = s(1) is not sufficient to ensure that N is a symmetric pseudoprime; we must also have s(2N) = s(2).

The first three symmetric pseudoprimes relative to polynomial (5) are listed below.

The next symmetric pseudoprime relative to polynomial (5) is 38503, which satisfies (3), making it the smallest determinate symmetric pseudoprime relative to (5). (In comparison, the Fibonacci polynomial has 18 determinate symmetric pseudoprimes less than 10000.)  There are only 69 determinate symmetric pseudoprimes relative to polynomial (5) less than 8(10)⁷, and these are listed in Table 5. Each of these satisfies the "splitting congruences" (3). It follows that congruence (4) (which is satisfied by half of all primes) is a sufficient primality criteria for integers less than 8(10)⁷.

The seven pseudoprimes appearing in parentheses in Table 5 can be distinguished from primes based on the values of the basis sequence elements b₀((N–1)/2) and b₁((N–1)/2). In a binary algorithm these two elements are always computed in the second-to-the-last step, so it's convenient to use these elements to strengthen the test. Letting m = (N–1)/2 we have

and

If N is a prime, it must satisfy either (3) or (4). If it satisfies (3) then (using the fact that gcd(N,c₂) = 1 for primes N > c₂) we have

Since N is assumed prime, it follows that either N divides b₁(m) or else gcd(N, b₁(m)) = 1. If N divides b₁(m), then clearly

On the other hand, if gcd(N, b₁(m)) = 1, it follows that

Since all of the psudoprimes in Table 5 satisfy (3), the above congruences are sufficient to exclude all 7 of the determinate pseudoprimes listed in parentheses.

Although we have not found any composites relative to (5) that satisfy (4), they presumably exist, so we will derive the congruence conditions on b₀((N–1)/2) and b₁((N–1)/2) for this case. Again letting m = (N–1)/2, we can rearrange the terms of (6) and then square to give    

Also, if we multiply (8) by c₁ and multiply (7) by c₂, we can eliminate the term –2c₁c₂b₀(m)b₁(m) from these two equations to give

Multiplying through by 4c₂b₁(m)², we can then substitute from equation (7) to yield the following quadratic in b₁(m)²:

Solving this for b₁(m)² gives the two possible values

which correspond to

Section 3.1 describes how the Legendre symbols [c₂/N] and [D/N] determine which of these two possible solutions applies for any given prime N.

2.3  Polynomials of Degree 3

By Proposition 6, a composite integer N co-prime to 6 is a symmetric pseudoprime relative to the third degree polynomial

iff all three of the congruences

are satisfied. If the polynomial is reversible (meaning that c₃ = ±1), then by Proposition 8 an odd composite integer N is a symmetric pseudoprime relative to f  iff the two congruences

are satisfied. Moreover, if f is reversible, Proposition 9 shows that a composite integer N is a symmetric pseudoprime relative to f  iff the two congruences

are satisfied.

The third degree polynomial that has recieved the most attention with respect to pseudoprime tests is

Following Shanks and Adams, we will refer to this as Perrin's polynomial. This particular polynomial seems to have been selected for study by Lucas and Perrin mainly because c₁ = 0, so s(p) is divisible by p for every prime p. Perrin also remarked that the sequence grows more slowly than the Fibonacci sequence, making some manual computations easier. The author's attention was drawn to (9) because its characteristic recurrence corresponds to the spiral tiling of equilateral triangles, just as the Fibonacci recurrence corresponds to the spiral tiling of perfect squares. These are the only two ways of partitioning the plane into a geometric progression of regular polygons.

Shanks and Adams found that, relative to Perin's polynomial, the smallest composite N such that s(N) ( 0 (mod N) is 271441. They also noted that Perrin's sequence is reversible, and that the primality test is strengthened by requiring the reverse congruence s(–N) = s(–1) (mod N). Composite integers N that satisfy s(±N) = s(±1) and four other congruences involving the terms s(±(N+1)) and s(±(N–1)) (mod N) were called "acceptable composites". (It was reported in [4] that, at least up to 50(10)⁹, the congruences involving s(±(N+1)) and s(±(N–1)) did not strengthen of the test.)  Based on the discussion in Section 1.4, it is clear that the composite integers N such that s(±N) = s(±1) (mod N) for a reversible cubic are precisely the symmetric pseudoprimes relative to that cubic.

Shanks and Adams found that the smallest symmetric pseudoprime relative to Perin's polynomial is 27664033. Subsequently Shanks, et al, listed all 55 symmetric pseudoprimes less than 50(10)⁹ relative to Perin's polynomial. The algorithm used to compute these results can be deduced from the material presented in Section 1.4. Since Perrin's polynomial has d = 3 and c_d = –1, the relations between the coefficient sequences and the symmetric functions with k = 3 give

Noting that s(0) = 3, that Warring's formula gives c₀(n) = 1 and c₁(n) = –s(n), and that

we have

which is equivalent to the "Doubling Rule" used by Shanks and Adams:

Furthermore, using the basis sequence relations from Section 1.2 with r = ±1, we have

These formulas are valid for all integers n, positive or negative, so they can operate on the "signature"

to compute s(N) and s(–N) (mod N) in log₂(N) steps, where each step requires 6 full multiplications.

The basis sequence algorithm described in Section 1.2 also requires d(d+1)/2 = 6 full multiplications per step, so in a sense the methods are equally efficient. However, for this particular case (reversible, third order) the "Doubling Rule" has the advantage of producing both s(N) and s(–N), whereas the basis sequence algorithm must include one additional step to compute s(2N) so as to complete the pseudoprime test. Also, the test based on s(N) and s(2N) is strictly applicable to odd integers only, whereas the test based on s(N) and s(–N) is applicable to all integers. On the other hand, the "Doubling Rule" has some drawbacks: (1) it requires manipulation and storage of 6 dynamic variables (the "signature"), versus only 3 for the basis sequence algorithm, (2) it applies only to reversible sequences, limiting it to recurrences with only d–1 congruence conditions and only one test per discriminant, and (3) it becomes progressively more complicated when generalized to recurrences of higher order. (We will illustrate this last point by presenting the "Doubling Rule" for 5th order recurrences in Section 2.5.)  In contrast, the basis sequence algorithm applies to non-reversible as well as reversible sequences, and to recurrences of any order.

For Perrin's sequence, the forward congruence s(N) = s(1) alone is sufficient to exclude most composites other than the symmetric pseudoprimes. The only ordinary pseudoprimes less than the first symmetric pseudoprime are

These numbers (which have a coincidental affinity for Mersenne prime factors) can be used to determine when certain summations take on integer values. This is based on the fact that the values of s(n) for Perrin's polynomial can be expressed in closed form as

where r = 0,1,.., or 5, and α,β are the least non-negative integers such that α = r (mod 2) and β = –r (mod 3). Clearly, the summation is an integer iff s(6N+r) = 0 (mod 6N+r). For example, the integer n = 16532714 = 6(2755452) + 2 satisfies the congruence s(n) = 0 (mod n), so 2755452 is the least positive integer N such that the summation

is an integer.

Perrin's polynomial is the fundamental reversible cubic with discriminant –23 (which is the smallest negative discriminant for a cubic). As explained by Shanks, et al, there are 12 reversible cubics with discriminant –23, but the corresponding recurrences are all of the form s(k) = s_Perrin's(mk) with m = ±1, ±2, ±3, ±4, ±5, or ±9. Therefore, every symmetric pseudoprime relative to Perrin's polynomial is also a symmetric pseudoprime relative to each of the other reversible polynomials of discriminant –23. However, since we are not restricted to reversible sequences, we can consider other polynomials with discriminant –23, such as

Even though the prime types relative to this polynomial are identical to the prime types relative to Perrin's polynomial, the only symmetric pseudoprimes less than 50(10)⁹ relative to both Perrin's polynomial and (10) are the four Carmichael numbers listed in [4]. This is because the periods of the two sequences modulo a given prime are not necessarily equal. The smallest symmetric pseudoprime relative to (10) of the form pq where p and q are both splitting primes is 3042763501 = (27581)(110321).

To give an example with a different discriminant, consider the non-reversible cubic

which has discriminant –135. Relative to this polynomial the smallest symmetric pseudoprime equal to the product of two splitting primes is 196049701 = (9901)(19801).

In Section 2.1 we gave an example of a cubic polynomial relative to which the integer 703 satisfies the first and second congruences but not the third. That polynomial was reducible, having the integer roots –17, 23, and 31. The same example can be given for an irreducible cubic by simply taking the coefficients modulo 703. Thus, relative to the irreducible polynomial

the integer 703 satisfies the first and second congruences but not the third.

2.4  Polynomials of Degree 4

Consider the quartic polynomial

By Proposition 8, a composite integer N co-prime to 6 is a symmetric pseudoprime relative to this polynomial if and only if

(We could also use the congruences on s(–N), s(N), and s(2N) to test any odd integer N.)  The initial values of the coefficient sequences are as follows:

The Galois group of (11) is the symmetric group S₄, so all 24 of the permutations of the roots are allowable, and the asymptotic proportion of prime types is as shown below.

Using the basis sequence algorithm of Section 1.2, we searched the splitting primes (i.e., primes of type {1₄}) relative to (11), and found that the smallest symmetric pseudoprime equal to the product of two splitting primes is

12282695011  =  (78367)(156733)

It's easy to show that if p and q are splitting primes then pq is a symmetric pseudoprime if and only if  b_k(p) = b_k(1) (mod q) and b_k(q) = b_k(1) (mod p).

An example of a non-reversible quartic is

Although this quartic is irreducible (according to Eisenstein's criterion), its Galois group is not the fully symmetric group. As a result, some root permutations are not allowable. Specifically, there are no primes of type {1₁3₁} relative to (12). The restricted nature of the roots of this polynomial also shows up in the fact that the general period of the prime type {4₁} always divides

This is because the four roots of (12) satisfy the relation

and so, noting that (12) is irreducible, we have

(The roots of (12) are discussed in Section 3. The resolvant cubic of this polynomial has one rational root, from which the permutation of the roots in the preceding expressions is determined.)

A complete search of odd integers shows that the smallest symmetric pseudoprime relative to (12) is

5351537  =  (1889)(2833)

The next symmetric pseudoprime relative to (12) that is a product of two splitting primes is

746331041  =  (15773)(47317)

2.5  Polynomials of Degree 5

A composite integer N co-prime to 120 is a symmetric pseudoprime relative to the fifth degree polynomial

if and only if all five of the congruences

are satisfied. In this section we will focus on the quintic polynomial

The discriminant of this polynomial is –4511 = –(13)(347), which is the smallest magnitude for any fully symmetric quintic [7]. The initial values of the coefficient sequences for this polynomials are listed below.

Since the Galois group of (13) is the fully symmetric S₅, all 120 of the root permutations are allowable, and all 7 of the prime types occur. Their asymptotic proportions are listed in the table below.

Relative to (13) the smallest symmetric pseudoprime equal to the product of two splitting primes is

2258745004684033  =  (27439297)(82317889)

The search for this number was carried out using the basis sequence algorithm described in Section 1.2. With this algorithm the computation of s(N) (mod N) requires 15(log₂N) full multiplications (mod N).

Since (13) is reversible, we could also have used a "Doubling Rule", analagous to that used by Shanks and Adams. For 5th order recurrences the basic doubling rule consists of the two formulas

where j = –c₅(1) = ±1. The part first comes directly from Warring's formula for c₂(n), which also gives s₁(4n) = s₁(2n)² – 2s₂(2n). To deduce the second part, we can set k = 3 in the relevant equation from Section 1 (with appropriate substitutions) to give an expression for s₁(3n) in terms of s₁(±2n) and s₁(±n) and s₂(n). Likewise we can set k = 4 to give an expression for s₁(4n) in terms of s₁(3n), s₁(2n), s₁(±n), and s₂(n). Then we eliminate s₁(3n) from thes two equations and substitute s₁(2n)² – 2s₂(2n) for s₁(4n), and s₁(n)² – 2s₂(n) for s₁(2n), to give the second part. The other equations needed to compute terms of the form s₁(2n+1) and s₂(2n+1) can be developed in the same way, although they involve a large number of elements from the s₁(±k) and s₂(±k) sequences (corresponding to the the "signature").

The type of any prime p with respect to a given polynomial f(x) can easily be determined by checking the number of linear and quadratic factors of f(x) modulo p. To find the number of (distinct) linear factors, we simply count the number of residues u in the range from 1 to p–1 such that f(u) = 0 (mod p). To find the number of quadratic factors, we count the number of residue pairs u,v such that (x² + ux + v)(x³ + Ax² + Bx + C) = f(x) modulo p for some integers A,B,C. This implies the conditions

Solving the first three for A, B, and C, and substituting into the last two, we have two necessary and sufficient conditions for  x² + ux + v  to divide f(x) modulo p. For example, with respect to the polynomial (13) we get the two conditions

Of course, if there are n₁ linear factors, we automatically get n₁(n₁–1)/2 non-primitive quadratic factors, so to give the number n₂ of primitive quadratic factors we must subtract n₁(n₁–1)/2 from the number of distinct pairs u,v that satisfy the quadratic conditions. Once the linear and quadratic factors have been divided out, what remains is a polynomial of degree m = 5 – n₁ – 2n₂. Clearly this must be an irreducible factor of degree 3, 4, or 5, so the numbers n₃, n₄, and n₅ of primitive cubic, biquadratic, and quintic factors can immediately be inferred.

With respect to the quintic f(x) given by equation (13) the prime p = 11 is of type 2₁3₁, which means that f(x) factors into a quadratic and a cubic in the field Z₁₁[x]_f. Specifically we have f(x) = g(x)h(x) where

As discussed in Section 1.7, it follows that the sequence x, x¹¹, x¹²¹... has period 6 in Z₁₁[x]_f, but the period is 3 in Z₁₁[x]_h, and the period is 2 in Z₁₁[x]_g. The actual terms of this sequence are listed below:

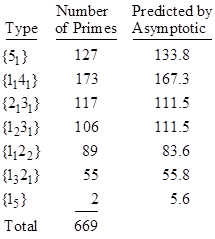
The types of all the primes less than 2000 relative to polynomial (13) are listed in Table 6.  Continuing on to determine the types for all 669 primes less than 5000, we find the following distribution:

The relativity scarcity of splitting primes (i.e., primes of the type 1₅) requires us to examine a larger number of primes in order to get a meaningful estimate of the asymptotic density. We find that, of the 9592 primes less than 100000, there are 75 splitting primes relative to (13), compared with a predicted 79.9. This confirms that the asymptotic density of splitting primes relative to this irreducible quintic is 1/120.

Return to Table of Contents