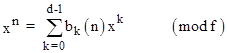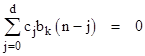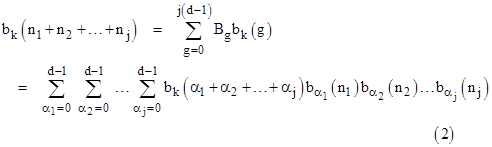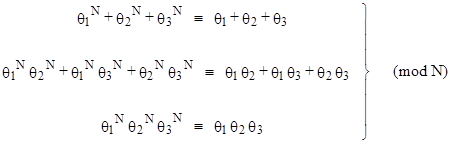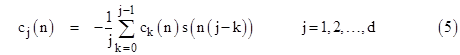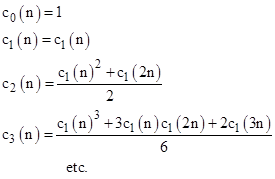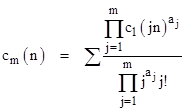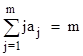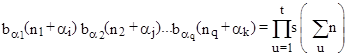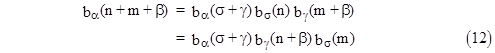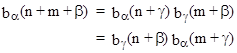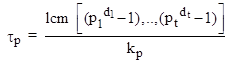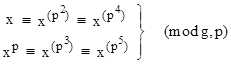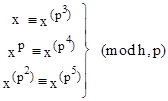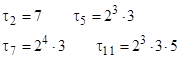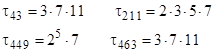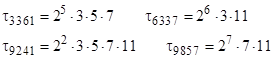1  Basic Propositions on Symmetric Pseudoprimes

1.1  Nomenclature and Definitions

Let Z[x] denote the set of polynomials (of finite degree) with integer coefficients. For any given monic polynomial f(x) in Z[x] of degree d, let Z[x]_f denote the elements of Z[x] modulo f. This signifies that two elements u(x), v(x) of  Z[x]  are equivalent in  Z[x]_f  if and only if  u(x) – v(x)  is divisible by f(x).

Proposition 1:  Each element of Z[θ]_f has a unique expression of degree d–1.

Proof:  Letting the modulus polynomial f(x) be

we see that any power of x greater than or equal to d can be expressed in terms of lower powers of x while preserving equivalence in  Z[x]_f  by making the substitution

Thus, every element of Z[x]_f can be reduced to a polyomial of degree ≤ d–1. The reduced polynomial is unique because if any two (distinct) such polynomials were equivalent, it would imply that their difference, a non-vanishing polynomial of degree d–1, is divisible by f(x), which is impossible. ◊

Thus each element of Z[x]_f can be expressed in the form

where a_i is in Z. If the coefficients a_k are considered as elements of Z_n (that is, the integers modulo n), then the set of polynomials of this form is denoted as Z_n(x)_f . For any  u,v in Z[x]  and n in Z, the notation u = v (mod f,n) signifies that u(x) and v(x) are equivalent elements of Z_n[x]_f .

The following generalization of Fermat's Little Theorem is the basis for the definition of a symmetric pseudoprime:

Proposition 2:  If p is a prime, then f(x^p) = 0 (mod f,p).

Proof:  Raising both sides of the congruence f(x) = 0 (mod f,p) to the power p, noting that all cross-product coefficients in the multinomial expansion are divisible by p, and that c_j^p = cj (mod p), we have the result. ◊

Definition 1:  A positive composite integer N such that f(x^N) = 0 (mod f;N) is called a symmetric pseudoprime relative to f.

An alternative definition in terms of symmetric functions is discussed in Section 1.3.

1.2  Basis Sequence Computations

For any non-negative integer n there is a unique set of integers b_k(n) such that

For each k the sequence of integers b_k(n) (n = 0,1,2,...) is called a basis sequence of f. Each basis sequence satisfies the fundamental recurrence relation of f

with the initial values

for j = 0, 1,.., d–1.

Proposition 3:  For any non-negative integers n₁, n₂,..., n_j and r, and for k = 0, 1,.., d–1, we have the identity

where summation from 0 through d–1 is implied over each α_i.

Proof:  By direct multiplication of the basis representations of each power of x we have

where B_g equals the sum of all products of the form

with α₁ + α₂ + ... + α_j = g. Substituting the representation for each power of x on the right side of the previous expression, the coefficient of x^k in the representation of  is given by

Clearly, this equality still holds if the argument of the left hand side and of the first term in the summation are both increased by any integer r. ◊

Notation:  Throughout this paper, whenever a Greek symbol appears both as a sequence index and in a sequence argument in a single product, summation over that symbol from 0 through d–1 is implied. Similarly, whenever a Latin symbol appears both as an index and an argument in a given product, summation over that symbol from 0 through d is implied (except when other summation limits are explicitly specified).

For computational purposes, a useful special case of (2) can be expressed using the index-argument convention as

By applying this formula log₂N times, with r equal to either 0 or 1 at each step according to the binary bits of N, we can efficiently compute the basis elements b_j(N) (j = 0, 1,.., d–1). The quantities b_j(α+β+r) are fixed constants for any given recurrence, so the only full multiplications required in each evaluation of (3) are the d(d+1)/2 distinct products of the form b_α(n)b_β(n).

Once the basis elements b_j(N) have been determined, the basis representations of x^2N, x^3N,.., x^dN can be found by applying the formula

with k = 2, 3,.., d. With these we can determine whether N satisfies the congruence f(x^N) = 0 (mod f,N), which is equivalent to the set of congruences

If N satisfies (4), then either N is a prime or N is a symmetric pseudoprime relative to f.

1.3  Elementary Symmetric Functions

Let θ₁, θ₂,... θ_d denote the complex roots of f, let f_n denote the monic polynomial whose roots are the nth powers of the roots of f, and let c_j(n) denote the coefficient of x^d–j in f_n(x). The jth elementary symmetric function of the roots of f_n is defined as the sum of all products of the roots taken j at a time, and is denoted by s_j(n). (For convenience we define s₀(n) = 1 for all n.)  It follows that

Hereafter, whenever s(n) is written without subscript, it is understood to signify the first symmetric function, i.e., the sum of the kth powers of the roots of f_n.

The index-argument summation convention previously defined for basis sequences also applies to both of the sequences s_j(n) and c_j(n), and to combinations of these sequences. For example, s(α)b_α(n) signifies the sum

Proposition 4:  The integer N is a prime or a symmetric pseudoprime relative to f if and only if s_j(N) = s_j(1) (mod N) for j = 0, 1, .., d.

Proof:  The condition s_j(N) = s_j(1) (mod N) for j = 0, 1,.., d implies that the coefficients of f and f_N are congruent (mod N). Therefore, since each x^N is a root of f_N, we also have f(x^N) = 0 (mod f,N), proving that N is a symmetric pseudoprime relative to f. Conversely, if N is a symmetric pseudoprime relative to f, we have f(θ_i^N) = 0 (mod f,N) for each root θ_i^N of f_N, which implies that the coefficients of f are congruent to the coefficients of f_N (mod N). ◊

In view of Proposition 4 we have the following alternative definition of symmetric pseudoprimes:

Definition 1':  Given a monic polynomial f of degree d with integer coefficients, a symmetric pseudoprime relative to f is defined as a positive composite integer N such that every elementary symmetric function of the Nth powers of the roots of f is congruent (mod N) to the same function of the first powers.

We will occassionally compare symmetric pseudoprimes with "ordinary" pseudoprimes, defined as follows:

Definition 2:  Given a monic polynomial f of degree d with integer coefficients, an ordinary pseudoprime relative to f is defined as a positive composite integer N such that the sum of the Nth powers of the roots of f is congruent (mod N) to sum of the first powers.

For example, if θ₁, θ₂, θ₃ are the roots of a cubic polynomial f, then an ordinary pseudoprime relative to f is a composite integer N co-prime to 6 and such that

whereas a symmetric pseudoprime relative to the same cubic f is a composite integer N such that

Proposition 5:  If N is a prime or a symmetric pseudoprime relative to f, we have s_j(kN) = s_j(k) (mod N) (j = 0, 1, .., d) for every positive integer k.

Proof:  The elementary symmetric functions of θ_i^k (i = 1, 2,.., d) can be expressed as polynomials in the elementary symmetric functions of the values θ_i. Similarly, the elementary symmetric functions of θ_i^Nk (k = 1, 2,.., d) can be expressed by the same polynomials in the elementary symmetric functions of the values θ_i^N. By Proposition 4 each elementary symmetric function of the θ_i is congruent (mod N) to the same function of the θ_i^N, so the elementary symmetric functions of the values θ_i^k are all congruent (mod N) to the same functions of the values θ_i^Nk. ◊

Proposition 6:  A positive composite integer N co-prime to d! is a symmetric pseudoprime relative to f  if and only if s(kN) = s(k) (mod N) for k = 1, 2,.., d.

Proof:  The necessity of the condition follows immediately from Proposition 5. To prove sufficiency, consider "Newton's relations"

for any integer n. Given the set of values s(n), s(2n),... s(dn) modulo some positive integer M, these relations uniquely determine the coefficients of f_n (mod M), provided that M is co-prime to d! (to ensure that all the divisions by j are unique modulo M). Therefore, if s(kN) = s(k) (mod N) for k = 1, 2,.., d, it follows that the coefficients of f are congruent (mod N) to the coefficients of f_N, which proves that for any u in Z[x] we have f(u) = f_N(u) (mod f,N). In particular,  f(θ^N) = f_N(θ^N) = 0  (mod f,N), so N is a symmetric pseudoprime relative to f. ◊

1.4  Reversible Sequences

If the constant coefficient c_d of f equals +1 or –1, then the values of c₁(k) are integers for all integers k, positive and negative. In this case, the sequence c₁(k) and the polynomial f are both called reversible.

Proposition 7:  If N is a prime or a symmetric pseudoprime relative to f, and the coefficient c_d of f is co-prime to N, then s_j(kN) = s_j(k) (mod N) (j = 0, 1,.., d) for every integer k, positive and negative.

Proof:  Since c_d is co-prime to N, the fundamental recurrence relations can be solved uniquely for s(n–d) and s(N(n–d)) respectively, and the corresponding coefficients remain congruent (mod N). Therefore, since the two sequences have congruent initial values and congruent recurrence coefficients (mod N), the sequences are entirely congruent (mod N) in both directions, positive and negative. It follows from equation (5) that the coefficients of the polynomials f_n and f_Nn are congruent for all n, positive and negative. ◊

In particular, Proposition 7 applies to every reversible sequence for any prime or symmetric pseudoprime N, because c_d = ±1 is obviously co-prime to N.

Proposition 8:  If f is reversible, then an odd positive composite integer N co-prime to (d–1)! is a symmetric pseudoprime relative to f if and only if s(kN) = s(k) (mod N) for k = 1, 2,.., d–1.

Proof:  The necessity follows from Proposition 7. To prove sufficiency, note that the d–1 specified congruences, together with the trivial congruence s(0N) = s(0), provide a complete set of congruent "initial values" for the two sequences s(kN) and s(k). Also, by the same argument used to prove Proposition 6, "Newton's relations" uniquely determine the coefficients c₁( ) through c_d–1( ) of the two recurrence relations. In addition, since c_d = ±1, we have c_d(k) = c_d(Nk) for every odd integer N. Thus, a complete set of initial values and all the recurrence coefficients of the two sequences are congruent (mod N), so we have s(k) = s(kN) (mod N) for every integer k. By Proposition 6, it follows that N is a symmetric pseudoprime relative to f. ◊

In the following proposition and proof we use the symbol {x} signify the greatest integer less than or equal to x.

Proposition 9:  If f is reversible, then an odd positive composite integer N co-prime to {d/2}! is a symmetric pseudoprime relative to f if and only if s(kN) = s(k) (mod N) for k = ±1, ±2,.., ε{d/2}, where ε = ±1 if d is odd and +1 if d is even.

Proof:  The coefficient c_d(n) of f_n is related to the roots of f by

Substituting (–1)^dc_d for (θ₁θ₂...θ_d) gives

Now, observing that the roots of  f _–n  are just the inverses of the roots of  f_n, we have

Given the values of s(kN) (mod N) for k = ±1, ±2,.., ε{d/2}, equation (5) uniquely determines the values (mod N) of c_j(N) and c_j(–N) for j = 1, 2,.., {d/2}, provided that N is co-prime to {d/2}! (to make the divisions by j unique (mod N)). Then by equation (6) we can use the c_j(–kN) to compute the values of c_j(kN) (mod N) for j = {d/2} + 1, .., d. Thus, the two sequences s(k) and s(kN) have a set of d consecutive values congruent (mod N) (including the equality with k = 0), and their recurrence coefficients are all congruent, so the entire sequences are congruent (mod N). ◊

For reversible sequences, the basis sequence formulas described in Section 1.2 can be extended to apply all integer arguments, positive and negative.

1.5  Coefficient Sequences

Although the basis sequence relations described in Section 1.2 provide an efficient and convenient means of evaluating the elements of the c₁(k) sequence for any given polynomial f, it is sometimes useful to have formulas expressed entirely in terms of the c₁(k) (or s(k)) sequence elements themselves. The fundamental recurrence for f_n can be written as

Since the value of k is arbitrary, we can set k = m + (r/n) for any integers m and r to give

Thus, the recurrence relation of f_n applies not only to the sequence c₁(nk) (k = 0, 1, 2,...), but also to the sequences c₁(nk+r) for any integer r. Furthermore, the coefficients of this recurrence relation can be expressed in terms of the c₁(nk) sequence elements by solving equation (5) explicitly for the c_j(n), which gives

In general, we have (Waring's formula)

where the summation is evaluated over all sets of m non-negative integers a_j such that

These equations can be used to implement a log₂N algorithm for computing c₁(N). For example, we can compute the recurrence coefficients c_k(n) for n = 1, 2, 4, 8,.., 2s, where s = [log₂n], in a "bootstrap" procedure, and then use these coefficients to compute c₁(N). Algorithms such as this can be applied to polynomials of any degree, but they generally involve more full multiplications per step, and more elaborate bookkeeping, than the basis sequence algorithm described in Section 1.2.

However, in some special cases it's possible to devise a coefficient sequence algorithm that is as efficient as a basis sequence algorithm. If the sequence is reversible, then the terms of c_j(n) in (7) can be replaced by ±c_d–j(–n) as given by equation (6). Thus, (7) can be expressed entirely in terms of the coefficient sequences c_j(±n) (or symmetric functions s_j(±n)) with j ≤ (d/2). This is particularly convenient for the case of a reversible cubic (see Section 1.3).

1.6  Relations Between Basis Sequences and Symmetric Functions

Given any sequence of values A(k) (k = 0, 1, 2,...) that satisfies the fundamental recurrence relation of f, we have

In particular,

Another expression for the first symmetric function s(n) is given by a "contraction" of the basis sequences

If we define the sequence of square matrices B_n (n = 0,1,2,..) with components given by B_n(i,j) = b_j(n+i), then s(n) can also be regarded as the trace of B_n.

It follows directly from (8) that

If the symbols α and β are permuted in the arguments, we have the slightly less obvious identity

Equations (9) and (10) are just two special cases of the following proposition.

Proposition 10:  Let {i,j,..,k} be a permutation of {1,2,..,q} composed of the cyclic components C₁, C₂, .., C_t. Then

where  signifies the sum of all the n_r such that r is in the cycle C_u.

Proof:  Proposition 3 gives both

and

Substituting from (11) into (12) (with k = n or m) gives

which is just the rule of multiplication for the components of matrices. Thus, equation (12) is equivalent to the matrix product B_n+m = B_nB_m = B_mB_n. Setting α = β in (12) gives, by contraction, equation (9). Repeated substitutions of either (11) or (12) leads to the general result. ◊

For example, the quantity

corresponds to the permutation [α,β,μ] → [μ,β,α], the cyclic  components of which are [α,μ] → [μ,α] and [β] → [β]. Thus, Proposition 10 gives the identity

1.7  Prime Types Relative to f(x)

We will classify each prime p relative to the polynomial  f  according to how  f  factors in Z_p[x]. The type of each prime p will be denoted by a symbol of the form , signifying that in the ring Z_p the polynomial f is the product of k₁ irreducible factors of degree 1, and k₂ irreducible factors of degree 2, and so on. If a subscript is zero, the term will normally be omited from the symbol. For example, if f is the product of one irreducible cubic factor and two linear factors in Z_p[x] we will say that p is a prime of type {1₂3₁} relative to f.

The type of the prime p relative to f is also related to the general period of the characteristic recurrence of f (mod p), defined as the least positive integer n such that b_j(n) = b_j(0) (mod p) (j = 0, 1,.., d–1). We will use the symbol τ_p to signify the general period of f (mod p).

Recall that Proposition 2 gives f(x^p) = 0 (mod f,p). By iterating the method of proof, this result can be extended to

for any non-negative integer k. Thus, each number  is a root of f in Z_p[x]_f.

Proposition 11:  If f is irreducible in Z_p[x], then the sequence of values  (mod f,p) has a period of d, i.e.,

Proof:  If p is a prime, then Z_p[x]_f is isomorphic to the finite field of order p^d. It is well known that if f is irreducible in Z_p, then the proposition follows. ◊

Since f is irreducible in Z_p[x], it follows that the ring of polynomials  Z_p[x]_f  possesses unique factorization, and therefore f has exactly d distinct factors in Z_p(θ)[x].

Dividing (13) by x gives

This shows that τ_p must divide p^d–1. For some common special cases this can be further refined by noting that the values of  (k = 0, 1,.., d–1) are the d roots of f in Z_p[x]_f. For example, since the product of the roots equals c_d, it follows that if c_d = (–1)^d, then τ_p divides 1 + p + .. + p^d–1 = (p^d – 1)/(p – 1). On the other hand, if c_d = –(–1)^d, then , so τ_p divides 2(p^d – 1)/(p – 1).

If f is reducible in Z_p[x], then the general period of its recurrence divides the least common multiple of the periods of the irreducible factors. For example, if p is a prime of type {2,3} relative to f, then τ_p divides lcm[(p² – 1), (p³ – 1)]. Since p² – 1 and p³ – 1 have the common factor p – 1, it follows that τ_p divides

In general, the sequence  has a period that divides the least common multiple of the degrees of the irreducible factors of f in Z_p[x]. Thus, we can write

where k_p is a divisor associated with the prime p.

The number of distinct roots of f in Z_p[x]_f can exceed the degree of f if f is reducible, because then unique factorization does not hold. For example, if p is of the type {2₁,3₁} relative to f, then each of the six values  is a distinct root of f in Z_p[x]_f . However, in related rings these six roots are not distinct. We have monic irreducible polynomials g and h of degree 2 and 3 respectively such that f = gh (mod p), and we find that the sequence   has period 2 in the ring Z_p[x]_g and period 3 in the ring Z_p[x]_h. Specifically we have

and

Letting α₁,α₂ denote the roots of g, and β₁,β₂,β₃ denote the roots of h, we can say the prime p induces the permutation [α₁,α₂,β₁,β₂,β₃] ® [α₂,α₁,β₂,β₃,β₁] on the roots of f. This permutation has two cyclic components, α_i and β_i, with periods 2 and 3 respectively. The periods of the cyclic components of the permutation induced by a prime p determines the "type" of p (relative to f). Furthermore, the cyclic structure corresponding to each type determines the asymptotic proportion of primes of that type. If each of the d! possible permutations of the d roots of f is equally likely to be induced by any given prime, we can see immediately the expected asymptotic proportion of primes of each type, based on the proportion of the permutations that possess each of the cyclic structures, corresponding to the partitions of d. For example, with d = 5 there are seven possible cyclic structures: 5, 4+1, 3+2, 3+1+1, 2+2+1, 2+1+1+1, and 1+1+1+1+1. The cyclic structure corresponding to "5" is just a single cycle of length 5, so the first element can go to one of four places, then one of three, then one of two, and then the one remaining place before it repeats. Hence there are 4! permutations with this cyclic structure, which implies that 4!/5! = 1/5 of all primes will be of type {5₁}. At the other extreme, the cyclic structure "1+1+1+1+1" is given by only one permutation, so only 1/5! = 1/120 of all primes would be splitting primes. In general, assuming each of the d! permutations is equally likely, the number of permutations for the prime type  is given by the multinomial coefficient

so the asymptotic density of each type is just 1 over the denominator.

However, for many polynomials of degree d the set of possible permutations of the roots is more restricted. The most general polynomial of degree d allows all d! permutations, in which case we say the (Galois) group of the polynomial is the fully symmetric group S_d , but there are also polynomials of degree d whose Galois group is a subgroup of S_d. For example, a quintic that is the product of 5 linear factors in Z[x] will obviously split completely in every ring Z_p[x]. In this case the basic Galois group is just the trivial identity group, I, with only one element, so every prime will be of the type {1₅}. On the other hand, some polynomials have Galois groups G that are intermediate between the identity group I and the fully symmetric group S_d. In those cases we can compute the asymptotic density of each "type" simply by computing the fraction of the permutations contained in G that have the cyclic structure of the respective type.

1.8  Recurrences Modulo Composites

Given the general period of the recurrence of f for each prime in the factorization of , the general period of the recurrence (mod n) is given by

where "lcm" signifies the least common multiple. For example, given the prime periods

relative to the polynomial f(x) = x³ – x – 1, the general period of the composite integer 360 = (2)³(3)²(5) equals the least common multiple of 2²(7), 3¹(13), and 5⁰(24). Therefore, τ₃₆₀ = 2184.

Using the equation above, we can determine highly "resonant" composite moduli relative to a given polynomial. For example, relative to x³ – x – 1 we have τ₄₄₉ = 224 = 2⁵(7), so the general period of the recurrence modulo 2⁶(449) equals the least common multiple of 2⁵(7) and 2⁵(7), which is just 224. This shows that all the elements of any given sequence satisfying the recurrence A_n = A_n–2 + A_n–3 fall into no more than 224 of the residue classes modulo 28736, which is less than 1% of all the residue classes.

To construct another example, we can begin with the fact that

and search for other primes whose periods divide this number. We find the following values

Therefore, all the elements of any given sequence satisfying the recurrence A_n = A_n–2 + A_n–3 fall into no more than 591360 distinct residue classes when evaluated modulo the number

which equals

In other words, the values of the sequence can fall into only 1 in (7.223)10²⁹ of all the residue classes.

Return to Table of Contents